1. Understanding the bending process: simple facts
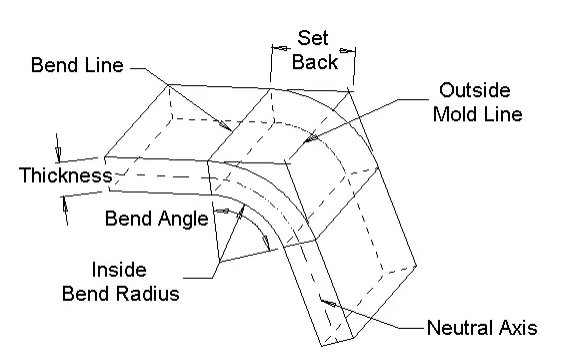
Bend Allowance = Angle * (T/ 180)*(Radius + K-factor *Thickness)Bend Compensation = Bend Allowance-(2 * Set Back)
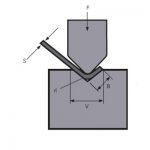
Inside Set Back = tan (Angle / 2) *Radius Outsideset Back = tan (Angle / 2)*(Radius + Thickness)

1) The radius obtained on a bent part affects the length to which we must cut that part (before bending).
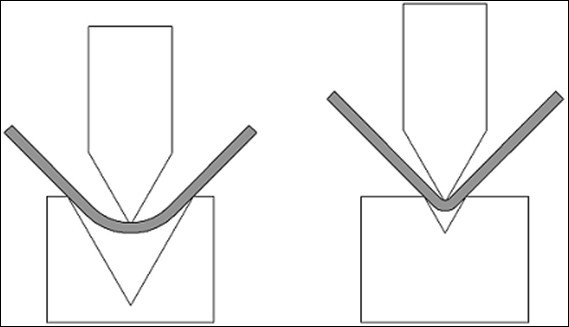
2) The radius obtained on bending depends 99% on the V opening we choose to work with.
Before designing the part and surely before starting to cut the blanks, we MUST know EXACTLY what V opening we will use to bend the part on the press brake.
2. How the radius affects blanks
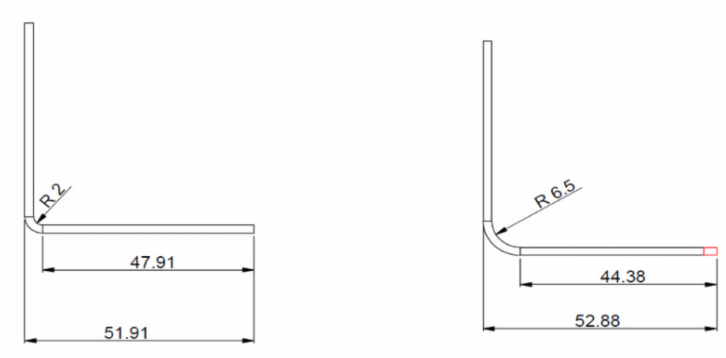
a larger radius will “push” the legs of our part toward the outside, giving the impression that the blank was cut “too long”.
a smaller radius will require a blank that must be cut “a little longer” than if the radius were larger.
3. Bending Allowance
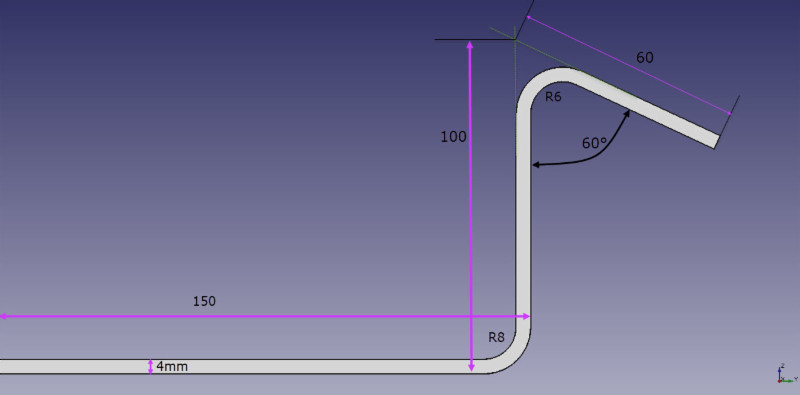
The unfolded blanks of the above figure would be calculated as follows:
B = 150 + 100 + 60 + BA1 + BA2
How to calculate BA1 and BA2:
Calculating the bending Allowance
The portion we need to reduce from both legs once overlapping by becoming flat, is what we commonly know as “bend allowance” (or BA in the equation).
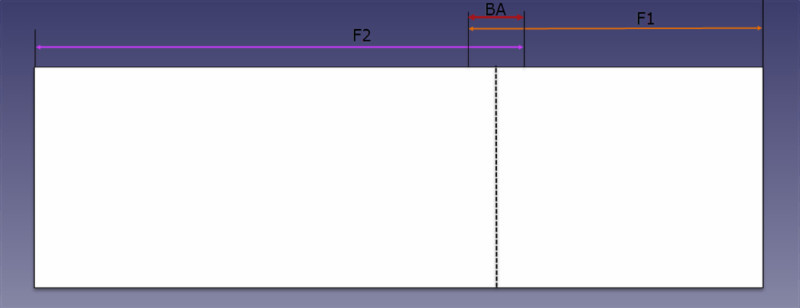
Bending allowance formula
BA formula for bends up to 90°
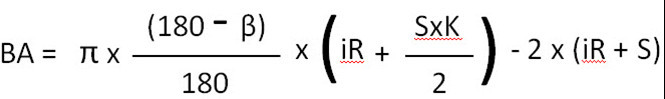
BA formula for bends from 91° to 165°
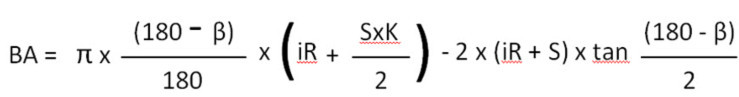
iR= Internal Radius
S=thickness
Β = angle
Π = 3,14159265….
K = K Factor
K factor
When bending on a press brake the inner part of the sheet metal is compressed while the outer part is extended.
This means that there is a portion of the sheet where the fibers are neither compressed nor extended. We call this portion the “neutral axis.”
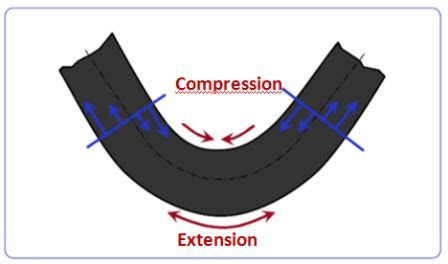
The distance from the inside of the bend to the neutral axis is what we call K factor.
This value comes with the material we buy and it can not be changed.
This value is expressed in fractions. The smaller the K factor, the closer the neutral axis will be to the inner radius of the sheet.
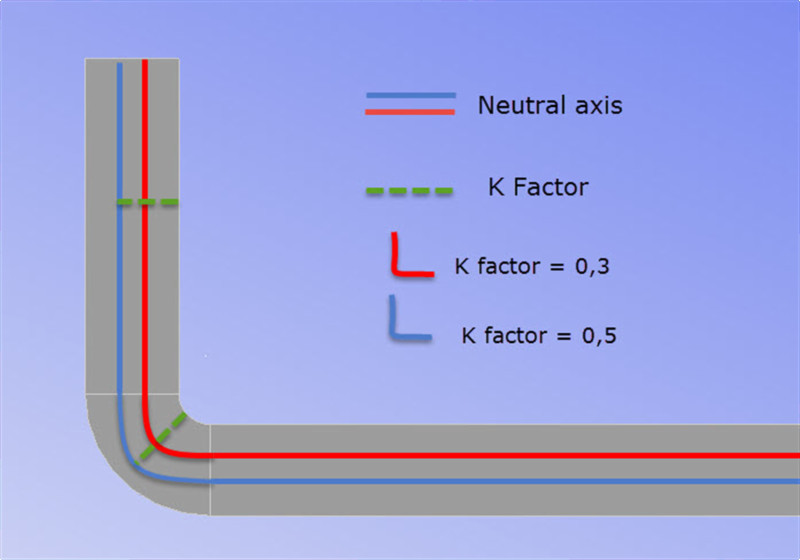
K factor = fine tuning
The K factor affects our unfolded blank. Not as much as the radius of the part, but we can think of it as a fine tuning calculations for blanks.
the smaller the K factor, the more material is extended and therefore “pushed out”…. which means our leg will become “larger”.
Estimating K factor
Most of the time we can estimate and adjust the K factor when fine tuning our blank calculations.
all we need to do are some tests (on the chosen V opening) and measure the radius of the part.
In case you need to determine a more precise K factor, below is the calculation for determining the exact K factor for your bend.

K factor: a formula
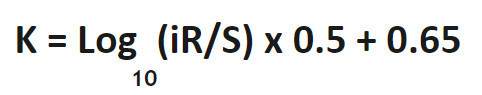
Solving the example:
B = 150 + 100 + 60 +BA1 + BA2
K factor estimation
B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
Both bends are 90° or less:
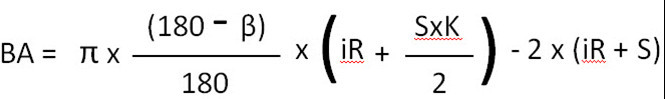
which means:
B1 = 3.14 x 0.66 x (6 + ((4×0.8)/2) – 2 x 10
B1 = -4.25
B2 = 3.14 x 0.5 x (8 + ((4×0.8)/2) – 2 x 12
B2 = -8.93
therefore:
B = 150 + 100 + 60 + (-4.25) + (-8.93)
B= 296.8mm